Содержание
Таблица гидравлических потерь для труб
Расчёт потерь напора воды в трубопроводе выполняется очень просто, далее мы подробно рассмотрим варианты расчёта.
Для гидравлического расчета трубопровода вы можете воспользоваться калькулятором гидравлического расчета трубопровода.
Вам посчастливилось пробурить скважину прямо около дома? Замечательно! Теперь вы сможете обеспечить себя и свой дом или дачу чистой водой, которая не будет зависеть от центрального водоснабжения. А это значит никакого сезонного отключения воды и бегания с вёдрами и тазиками. Нужно только установить насос и готово! В настоящей статье мы поможем вам рассчитать потери напора воды в трубопроводе, и уже с этими данными можно смело покупать насос и наслаждать, наконец, своей водой из скважины.
Из школьных уроков физики понятно, что вода, текущая по трубам, в любом случае испытывает сопротивление. Величина этого сопротивления зависит от скорости потока, диаметра трубы и гладкости её внутренней поверхности. Сопротивление тем меньше, чем меньше скорость потока и больше диаметр и гладкость трубы. Гладкость трубы зависит от материала, из которого она изготовлена. Трубы из полимеров более гладкие, чем стальные трубы, а также они не ржавеют и, что немаловажно, дешевле других материалов, не уступая при этом в качестве. Вода будет испытывать сопротивление, двигаясь даже по полностью горизонтальной трубе. Однако чем длиннее сама труба, тем менее значительны будут потери напора. Что ж, приступим к расчету.
Потери напора на прямых участках трубы.
Чтобы подсчитать потери напора воды на прямых участках труб использует уже готовую таблицу, представленную ниже. Значения в этой таблице указаны для труб, изготовленных их полипропилена, полиэтилена и других слов, начинающихся с «поли» (полимеров). Если же вы собираетесь установить стальные трубы, то необходимо умножить приведённые в таблице значения на коэффициент 1,5.
Данные приведены на 100 метров трубопровода, потери указаны в метрах водного столба.
Внутренний диаметр трубы, мм
Расчет гидравлических потерь давления в трубопроводе из пластмасс
Расчет гидравлических потерь давления в трубопроводе из пластмасс
Гидравлический расчет является важной составляющей процесса выбора типоразмера трубы для строительства трубопровода. В нормативной литературе по проектированию этот ясный с точки зрения физики вопрос основательно запутан. На наш взгляд, это связано с попыткой описать все варианты расчета коэффициента трения, зависящего от режима течения, типа жидкости и ее температуры, а также от шероховатости трубы, одним (на все случаи) уравнением с вариацией его параметров и введением всевозможных поправочных коэффициентов. При этом краткость изложения, присущая нормативному документу, делает выбор величин этих коэффициентов в значительной степени произвольным и чаще всего заканчивается номограммами, кочующими из одного документа в другой.
С целью более подробного анализа предлагаемых в документах методов расчета представляется полезным вернуться к исходным уравнениям классической гидродинамики (1).
Потеря напора, связанная с преодолением сил трения при течении жидкости в трубе, определяется уравнением: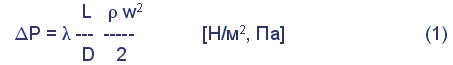
где: L и D длина трубопровода и его внутренний диаметр, м; ? — плотность жидкости, кг/м 3 ; w – средняя объемная скорость, м/сек, определяемая по расходу Q, м 3 /сек: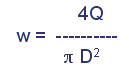
λ – коэффициент гидравлического трения, безразмерная величина, характеризующая соотношение сил трения и инерции, и именно ее определение и есть предмет гидравлического расчета трубопровода. Коэффициент трения зависит от режима течения, и для ламинарного и турбулентного потока определяется по-разному.
Для ламинарного (чисто вязкого режима течения) коэффициент трения определяется теоретически в соответствии с уравнением Пуазейля:
λ = 64/Re (2)
где: Re – критерий (число) Рейнольдса.
Опытные данные строго подчиняются этому закону в пределах значений Рейнольдса ниже критического (Re 100000 предложено много расчетных формул, но практически все они дают один и тот же результат [1 — 3].
На рис.1 показано, как «работают» уравнения (2) – (4) в указанном диапазоне чисел Рейнольдса, который достаточен для описания всех реальных случаев течения жидкости в гидравлически гладких трубах.
Рис. 1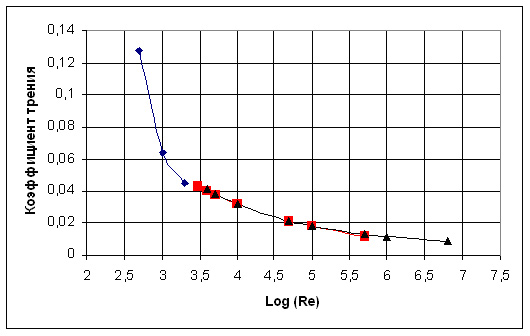
Шероховатость стенки трубы влияет на гидравлическое сопротивление только при турбулентном потоке, но и в этом случае, из-за наличия ламинарного пограничного слоя существенно сказывается только при числах Рейнольдса, превышающих некоторое значение, зависящее от относительной шероховатости ξ/D, где ξ – расчетная высота бугорков шероховатости, м.
Труба, для которой при течении жидкости выполняется условие:
считается гидравлически гладкой, и коэффициент трения определяется по уравнениям (2) – (4).
Для чисел Re больше определенных неравенством (5) коэффициент трения становится величиной постоянной и определяется только относительной шероховатостью по уравнению: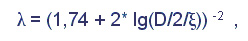
которое после преобразования дает: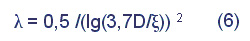
Гидравлическое понятие шероховатости не имеет ничего общего с геометрией внутренней поверхности трубы, которую можно было бы инструментально промерить. Исследователи наносили на внутреннюю поверхность модельных труб четко воспроизводимую и измеряемую зернистость, и сравнивали коэффициент трения для модельных и реальных технических труб в одних и тех же режимах течения. Этим определяли диапазон эквивалентной гидравлической шероховатости, которую следует принимать при гидравлических расчетах технических труб. Поэтому уравнение (6) точнее следует записать: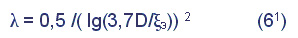
где: ξ э — нормативная эквивалентная шероховатость (Таблица 1).
Еще раз о стальных и металлополимерных трубопроводах
А. С. Жданов, старший преподаватель НовГУ имени Ярослава Мудрого
В настоящее время в системах отопления, холодного и горячего водоснабжения все большее распространение получают трубопроводы из полимерных материалов. Преимущества их очевидны: коррозионная стойкость, малый вес, простота монтажа и т. д. Зачастую реклама делает акцент на малые гидравлические и тепловые потери из-за низких значений коэффициентов эквивалентной шероховатости и теплопроводности полимеров. При этом даются рекомендации по уменьшению диаметров металлополимерных трубопроводов [1], а также по отсутствию необходимости их изоляции по сравнению со стальными. Ошибочность подобных утверждений была показана в статье В. И. Сасина «Применение полимерных труб в системах отопления» [2], в которой приведены результаты тепловых и гидравлических испытаний металлополимерных труб. Однако информация о низких гидравлических сопротивлениях и тепловых потерях пластиковых труб в осторожных формулировках периодически появляется в технических статьях, например в [3, 4].
Цель данной статьи – провести сравнительный анализ гидравлических и тепловых характеристик стальных, металлопластиковых и армированных полипропиленовых трубопроводов, используя классические уравнения гидравлики и теплопередачи.

Гидравлические характеристики трубопроводов
Определим удельные гидравлические потери различных трубопроводов при условиях, наиболее характерных для внутренних инженерных систем отопления и водоснабжения, используя уравнение Дарси–Вейсбаха:
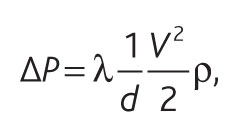 (1)
(1)
где ΔP – удельные потери давления, Па/м;
λ – коэффициент гидравлического трения;
V – скорость перемещаемой среды, м/с;
d – внутренний диаметр трубопровода, м;
ρ – плотность перемещаемой среды, кг/м 3 .
Для коэффициента гидравлического трения воспользуемся универсальной формулой Альт-шуля:
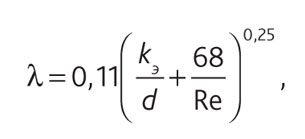 (2)
(2)
где kэ – эквивалентная шероховатость труб, м;
Re = V×d/v – число Рейнольдса,
v – коэффициент кинематической вязкости, м 2 /с.
Уравнение (1) с учетом (2) примет вид:
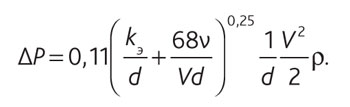 (3)
(3)
Для определенности примем при расчетах параметры воды при 65 °С: плотность 980 кг/м 3 , коэффициент кинематической вязкости 0,447×10 –6 м 2 /с. Значение эквивалентной шероховатости внутренней поверхности трубопроводов согласно [5] составляет не менее 0,01 мм для труб из полимерных материалов, 0,5 мм для стальных труб при зависимом присоединении систем внутреннего теплоснабжения к тепловой сети.
На рис. 1 представлены графические зависимости удельных потерь давления от скорости движения теплоносителя для различных диаметров трубопроводов, построенные на основании уравнения (3).
Полученные результаты расчетов, указанные на графиках (рис. 1), хорошо согласуются с данными удельных потерь давления, приведенными на диаграммах различных источников, например: для полипропиленовых [6], для стальных труб [7].
Из графиков видно, что при скоростях движения теплоносителя 0,2÷1 м/с, характерных для отопительных систем [8], удельные потери давления стальных и армированных полипропиленовых труб в рассматриваемом диапазоне диаметров 20÷50 мм практически совпадают. Такое незначительное отличие в удельных потерях давления стальных и армированных полипропиленовых трубопроводов, несмотря на огромную разницу (в 50 раз) в значениях коэффициентов эквивалентной шероховатости, объясняется существенным различием в значениях внутренних диаметров труб (табл. 1).
| Технические размеры | Труба стальная | Труба полипропиленовая армированная | Труба металлопластиковая | ||||||
| Типоразмер трубопровода | 20х2,8 | 32х3,2 | 57х3,5 | 20х3,4 | 32х5,4 | 50х8,3 | 20х2,0 | 32х3,0 | 50х4,0 |
| Наружный диаметр, мм | 26,8 | 42,3 | 57,0 | 20,0 | 32,0 | 50,0 | 20,0 | 32,0 | 50,0 |
| Толщина стенки, мм | 2,8 | 3,2 | 3,5 | 3,4 | 5,4 | 8,3 | 2,0 | 3,0 | 4,0 |
| Внутренний диаметр, мм | 21,2 | 35,9 | 50,0 | 13,2 | 21,2 | 33,4 | 16,0 | 26,0 | 42,0 |
Например, у стальной водогазопроводной трубы 20×2,8 (первая цифра в обозначении определяет диаметр условного прохода) внутренний диаметр составляет 21,2 мм, у армированной полипропиленовой 20×3,4 (первая цифра в обозначении определяет наружный диаметр) – 13,2 мм, т. е. площадь поперечного сечения для прохода теплоносителя у данной полипропиленовой трубы в 2,58 раза меньше, чем у стальной.
Следует отметить, что основная задача системы тепло- или водоснабжения – обеспечение потребителей необходимым количеством теплоносителя. Поэтому более корректно сравнивать гидравлические характеристики различных трубопроводов не при равных скоростях движения воды, а при равных расходах.
Определим скорость движения воды следующим образом:
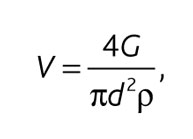 (4)
(4)
где G – массовый расход теплоносителя, кг/с.
Используя формулу (4), выразим удельные потери давления (3) через массовый расход теплоносителя:
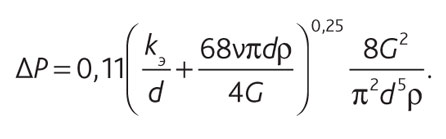 (5)
(5)
На рис. 2 представлены графические зависимости удельных потерь давления от массового расхода теплоносителя для различных диаметров трубопроводов, построенные на основании уравнения (5).
Из графиков (рис. 2) видно, что при равных расходах теплоносителя из-за меньшего внутреннего диаметра, несмотря на маленькое значение эквивалентной шероховатости внутренней поверхности материала, удельные потери давления пластиковых трубопроводов по сравнению со стальными имеют существенно большие значения. Из этого следует, что рекомендации по снижению диаметров при замене стальных трубопроводов на металлополимерные являются неправомерными. Более того, при подобной замене, чтобы гидравлические потери не превышали прежнего значения, диаметр необходимо увеличивать на один типоразмер для металлопластиковых и на два типоразмера для армированных полипропиленовых трубопроводов (рис. 3).
Тепловые характеристики трубопроводов
Найдем плотность теплового потока открыто проложенных неизолированных горизонтальных трубопроводов из различных материалов согласно [9]:
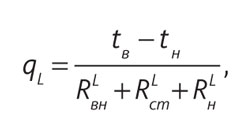 (6)
(6)
где qL – линейная плотность теплового потока, Вт/м;
tв – температура среды внутри трубопровода, °С;
tн – температура окружающей среды, °С;
Rвн L – линейное термическое сопротивление теплоотдаче внутренней стенки трубопровода, (м•°С) /Вт;
Rст L – линейное термическое сопротивление цилиндрической стенки трубопровода, (м•°С)/Вт;
Rн L – линейное термическое сопротивление теплоотдаче наружной стенки трубопровода, (м•°С)/Вт.
Определим линейные термические сопротивления следующим образом:
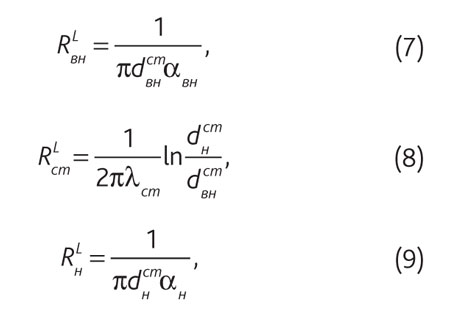
где αн, αвн. – коэффициенты теплоотдачи наружной и внутренней поверхностей трубопровода, Вт/(м 2 •°С);
λст – коэффициент теплопроводности материала стенки трубопровода, Вт/(м•°С);
dн ст , dвн ст – наружный и внутренний диаметры трубопровода, м.
Для определенности примем при расчетах температуру среды внутри трубопровода 65 °С, температуру окружающей среды 20 °С, коэффициент теплопроводности стали 52 Вт/(м•°С), коэффициент теплопроводности полипропилена 0,24 Вт/(м•°С), коэффициент теплопроводности сшитого полиэтилена 0,45 Вт/(м•°С), коэффициент теплоотдачи наружной поверхности трубопровода 10 Вт/(м 2 •°С). Сопротивление теплоотдаче внутренней стенки трубопровода для жидкой среды является пренебрежимо малым, в расчете учитывать не будем. Наружные и внутренние диаметры трубопроводов приведены в табл. 1. Результаты расчетов линейной плотности теплового потока для трубопроводов из различных материалов по зависимостям (6) – (9) приведены на диаграммах (рис. 4). Следует отметить, что полученные расчетным путем данные линейной плотности теплового потока оказались в среднем на 25 % меньше значений, приведенных в таблице [10] для металлических трубопроводов.
Ранее было показано, что при замене стальных труб пластиковыми и выполнении условия непревышения удельных потерь давления при равных расходах теплоносителя типоразмер (диаметр) последних следует увеличивать, что, в свою очередь, ведет к повышению площади поверхности теплообмена с окружающим воздухом. Из диаграмм (рис. 4) видно, что значения удельных плотностей тепловых потоков (выделены в рамку) для стальной трубы – 20×2,8, металлопластиковой – 26×3,0 и армированной полипропиленовой – 32×5,4 сопоставимы друг с другом. Следовательно, утверждения о повышении энергоэффективности инженерных систем из-за снижения тепловых потерь при использовании пластиковых труб в данном случае также являются неправомочными.
Рассмотрим вопрос о необходимости изолирования трубопроводов из полимерных материалов на конкретном примере. Проверим условие образования конденсата на поверхности полипропиленовой трубы 20×3,4 системы холодного водоснабжения. Примем тем-пературу воды +5 °С, температуру воздуха в помещении +20 °С, относительную влажность 60 %. Коэффициент теплопроводности полипропилена составляет 0,24 Вт/(м•°С), коэффициент теплоотдачи наружной поверхности трубопровода 7 Вт/(м 2 •°С). Расчет выполним согласно [9, 11], пренебрегая сопротивлением теплоотдаче внутренней стенки трубы для жидкой среды.
Определим линейные термические сопротивления:
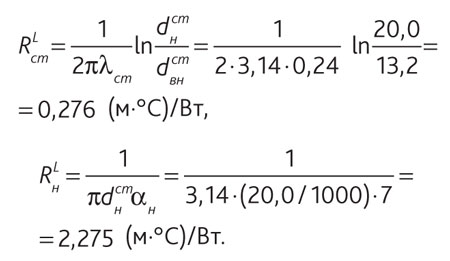
Линейная плотность теплового потока составит:
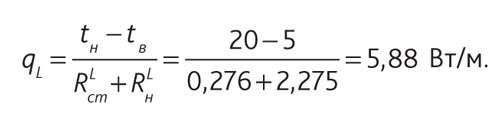
Температура на наружной поверхности стенки трубы равна:
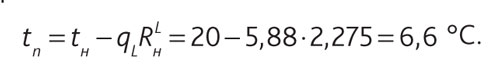
Парциальное давление насыщенного пара:
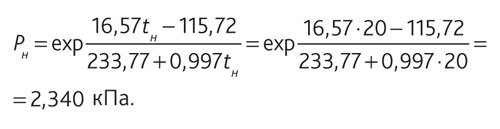
Парциальное давление водяного пара:
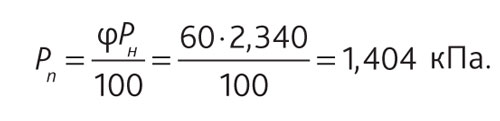
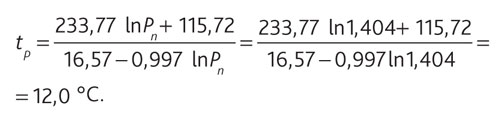
Температура на поверхности неизолированного трубопровода при рассматриваемых условиях tп = 6,6 °С меньше температуры точки росы окружающего воздуха tр = 12,0 °С, что является условием образования конденсата. Таким образом, рекомендации об отсутствии необходимости изолирования пластиковых трубопроводов по сравнению со стальными в данном случае также не подтверждаются расчетом.
Заключение
Проведен сравнительный анализ тепловых и гидравлических характеристик трубопроводов из различных материалов, используя классические уравнения гидравлики и теплопередачи. Расчетом показано, что, несмотря на низкие значения эквивалентной шероховатости и теплопроводности полимеров, утверждения, связанные со снижением гидравлических и тепловых потерь и отсутствием необходимости изолирования пластиковых трубопроводов по сравнению со стальными, во многих случаях являются неправомочными и носят, скорее, рекламный характер. Для принятия правильных проектных решений проектировщикам следует внимательнее относиться к подобным рекомендациям, опираться на грамотные технические расчеты и проверенные экспериментальные данные.
Литература
- Олейников Ю. Д. Особенности монтажа полипропиленовых труб // С.О.К. – 2011. – № 7.
- Сасин В. И. Применение полимерных труб в системах отопления // Сантехника. – 2011. – № 3.
- Наумов А. Л. Инженерные системы малоэтажных зданий. Ч. 2. Системы климатизации // АВОК. – 2014. – № 2.
- Шонина Н. А. Применение пластиковых труб для систем водоснабжения и водоотведения при капитальном ремонте зданий // Сантехника. – 2015. – № 4.
- СП 60.13330.2012 «Отопление, вентиляция и кондиционирование воздуха. Актуализированная редакция СНиП 41-01–2003». – М., 2012.
- СП 40-101–96 «Проектирование и монтаж трубопроводов из полипропилена «Рандом сополимер». – М., 1996.
- Соколов Е. Я. Теплофикация и тепловые сети: Учеб. для вузов. 7-е изд., стереотип. – М.: Изд. МЭИ, 2001.
- Щекин Р. В., Кореневский С. М., Бем Г. Е. и др. Справочник по теплоснабжению и вентиляции. 4-е изд., перераб. и доп. – Киев: Будiвельник, 1976.
- СП 61.13330.2012 «Тепловая изоляция оборудования и трубопроводов. Актуализированная редакция СНиП 41-03–2003». – М., 2012.
- Рекомендации по применению секционных радиаторов итальянского предприятия GLOBAL. 3-я редакция. – М.: Изд. Научно-техн. фирмы ООО «Витатерм», 2010.
- СТО 59705183–001–2007 «Стандарт организации. Конструкции тепловой изоляции для оборудования и трубопроводов с применением теплоизоляционных пенополиэтиленовых изделий Energoflex. Проектирование и монтаж». 7-е изд., испр. и доп. – М., 2015.
Поделиться статьей в социальных сетях:
Все иллюстрации приобретены на фотобанке Depositphotos или предоставлены авторами публикаций.

Статья опубликована в журнале “Сантехника” за №3’2016
 распечатать статью —>
распечатать статью —>  pdf версия
pdf версия
Формулы для расчетов потери давления в трубопроводе
Любая трубопроводная коммуникация имеет не только прямолинейные участки, но и повороты, ответвления, для создания которых используются различные фитинги.
А для регулирования потока рабочей среды устанавливается запорная арматура. Всё это создаёт сопротивление, поэтому очень важно перед тем, как приступать к монтажу трубопровода, необходимо выполнить ряд расчётов, в том числе определить гидравлическое сопротивление.
Это позволит в будущем сократить теплопотери и, соответственно, избежать лишних энергозатрат.
Гидравлический расчёт выполняется с целью:
- Вычисления потерь давления на конкретных отрезках системы отопления;
- Определения оптимального диаметра трубопровода с учётом рекомендованной скорости перемещения рабочего потока;
- Расчёта тепловых потерь и величины наименьшего давления в трубопроводе;
- Правильного выполнения увязки параллельно расположенных гидравлических ветвей и закреплённой на ней запорной арматуры.
Во время движения по замкнутому контуру рабочему потоку приходится преодолевать определённое гидравлическое сопротивление. Причём с увеличением его значения, должна увеличиваться мощность насоса.
Только правильные расчёты помогут выбрать оптимальный вариант насоса.
Нет смысла покупать слишком мощное оборудования для трубопроводов с низким гидравлическим сопротивлением, ведь, чем больше мощность, тем выше энергозатраты.
А если мощность будет, наоборот, недостаточной, то насосное оборудование не сможет обеспечить достаточный напор теплоносителя, что приведёт к увеличению тепловых потерь.
- Это безмерная величина, показывающая, каковы потери удельной энергии.
- Ламинарное перемещение рабочего потока
- При ламинарном (равномерном) перемещении рабочей среды по трубопроводу круглого сечения потери давления по длине вычисляется по формуле Дарси-Вейсбаха:

- Где:
- – потери давления по длине;
- – коэффициент гидравлического сопротивления;
- v – скорость движения рабочей среды;
- g – ускорение силы тяжести;
- d – диаметр трубопроводной магистрали.
- Практически определено, что на коэффициент гидравлического сопротивления непосредственное влияние оказывает число Рейнольдса (Re) – безмерная величина, которая характеризует поток жидкости и выражается отношением динамического давления к касательному напряжению.
- Если Re меньше, чем 2300, то для расчёта применяется формула:
- Для трубопроводов в форме круглого цилиндра:
- Для трубопроводных коммуникаций с другим (не круглым) сечением:
- Где А=57 – для квадратных труб.
- Турбулентное течение рабочего потока
- При турбулентном (неравномерном, беспорядочном) перемещении рабочего потока коэффициент сопротивления вычисляют опытным путём, как функцию от Re. Если необходимо определить коэффициент гидравлического сопротивления для магистрали круглого сечения с гладкими поверхностями при
![]()
![]()
- В случае турбулентного перемещения рабочей среды на величину коэффициента трения влияет число Рейнольдса (характер течения) и насколько гладкая внутренняя поверхность трубопроводной коммуникации.
- Коэффициент местного сопротивления
- Это безмерная величина, которая устанавливается экспериментальным путём с помощью формулы:
![]()
- Где:
- – коэффициент местного сопротивления;
- – потеря напора;
- – отношение скорости потока к ускорению силы тяжести – скоростной поток.
- При неизменной скорости перемещения рабочей среды по всему сечению применяется формула:
![]()
Для фитингов из ППР:
| Муфта | 0,25 | |
| Муфта переходная | Уменьшение на 1 размер | 0,40 |
| Уменьшение на 2 размер | 0,50 | |
| Уменьшение на 3 размер | 0,60 | |
| Уменьшение на 4 размер | 0,70 | |
| Угольник 90° | 1,20 | |
| Угольник 45° | 0,50 | |
| Тройник | Разделение потока | 1,20 |
| Соединение потока | 0,80 | |
| Крестовина | Соединение потока | 2,10 |
| Разделение потока | 3,70 | |
| Муфта комб. вн. рез. | 0,50 | |
| Муфта комб. нар. рез | 0,70 | |
| Угольник комб. вн. рез. | 1,40 | |
| Угольник комб. нар. рез. | 1,60 | |
| Тройник комб. вн. рез. | 1,40 – 1,80 | |
| Вентиль | 20 мм | 9,50 |
| 25 мм | 8,50 | |
| 32 мм | 7,60 | |
| 40 мм | 5,70 |
Для полиэтиленовых труб
| Сталь новая 133×5 | 60 | 1,4 | 3,6 |
| Сталь старая 133×5 | 60 | 1,4 | 6,84 |
| ПЭ 100 110×6,6 (5ЭР 17)/td> | 60 | 2,26 | 4,1 |
| ПЭ 80 110×8,1 (ЗйР 13,6) | 60 | 2,41 | 4,8 |
| Сталь новая 245×6 | 400 | 2,6 | 4,3 |
| Сталь старая 245×6 | 400 | 2,6 | 7,0 |
| ПЭ 100 225×13,4 (50 В 17) | 400 | 3,6 | 4,0 |
| ПЭ 80 225×16,6 (ЗЭК 13,6) | 400 | 3,85 | 4,8 |
| Сталь новая 630×10 | 3000 | 2,85 | 1,33 |
| Сталь старая 630×10 | 3000 | 2,85 | 1,98 |
| ПЭ 100 560×33,2 (ЗЭК 17) | 3000 | 4,35 | 1,96 |
| ПЭ 80 560×41,2 (ЗЭК 13,6) | 3000 | 4,65 | 2,3 |
| Сталь новая 820×12 | 4000 | 2,23 | 0,6 |
| Сталь старая 820×12 | 4000 | 2,23 | 0,87 |
| ПЭ100 800×47,4 (ЗЭК 17) | 4000 | 2,85 | 0,59 |
| ПЭ 80 800×58,8 (ЗЭР 13,6) | 4000 | 3,0 | 0,69 |
Для бесшовных стальных труб
| Ламинарный | или | |
| Переходный | Проектирование трубопроводов не рекомендуется | |
| Турбулентный | 1-я область | (ф-ла Блазиуса) |
| 2-я область | | |
| 3-я область | |
Для металлопластиковых труб
| Тройник разделения потока | 7,6 |
| Тройник проходной | 4,2 |
| Тройник противоположные потоки при разделении потока | 8,5 |
| Тройник противоположные потоки при слиянии потока | 8,5 |
| Угол 90° | 6,3 |
| Дуга | 0,9 |
| Редукционный переход | 6,3 |
| Установочный уголок | 5,4 |
С точки зрения гидравлического сопротивления, наиболее оптимальными являются трубопроводные системы с гладкой внутренней стенкой:
Пластиковые трубы произведенные в Германии, широкого спектра применения.
Система отлично подходит для систем горячего и холодного водоснабжения и отопления, как в частных, так и промышленных масштабах. Так же используется для транспортировки химических сред.
Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
- Пластиковые трубы произведенные в Германии, широкого спектра применения.
- Трубопроводная система из инновационного материала fusiolen, специально разработанная для систем холодоснабжения, обогрева поверхностей, транспортировки агрессивных сред и сжатого воздуха, а также для систем геотермальной энергетики.
- Имеет гладкую внутреннюю стенку, что обеспечивает низкий коэффициент гидравлического сопротивления.
Здравствуйте. Помогите подобрать производительность насоса(давление ит.д) с учетом гидравлического сопротивления трубопроводов – результат: время перекачки 80 литров раствора NaOH плотностью 1,48 кг/л не должна быть выше 2 минут. DN32, длина трубопровода 17м Уважаемый Юрий! Информация направлена на Вашу почту. Помогите рассчитать потерю давления на газопроводе с начальным диаметром dn80, через 0,1 м становиться dn32 и тянется 10 м Уважаемый Андрей! Информация направлена на вашу почту! Добрый день, помогите рассчитать сопротивление резиновых трубопроводов. Уважаемый Николай! Информация направлена на Вашу почту. Что такое м/100м (в потерях напора)? Уважаемый Павел! Данная колонка с данными отображает потери напора в метрах, на 100 метров прямого трубопровода (м/100м).
Расчет потерь напора в трубопроводах
Главная / Технические статьи / Расчет потерь напора в трубопроводах
- В процессе течения нефтепродуктов имеют место потери напора на трение hτ и местные сопротивления hMC.
- Потери напора на трение
- Потери напора на трение при течении ньютоновских жидкостей в круглых трубах определяются по формуле Дарси—Вейсбаха

- где λ — коэффициент гидравлического сопротивления; L, D — соответственно длина и внутренний диаметр трубопровода; W — средняя скорость перекачки; g — ускорение силы тяжести.
- Величина коэффициента гидравлического сопротивления λ в общем случае зависит от числа Рейнольдса Re = W • D/v и относительной шероховатости труб ε = kэ/D (здесь v — кинематическая вязкость нефтепродукта при температуре перекачки; кэ — эквивалентная шероховатость стенки трубы).
- При ламинарном режиме перекачки (Re = ReKp) расчет λ выполняется по формуле Стокса
- λ = 64/Re
- В переходной зоне (ReKp ReII) расчет λ обычно ведут по формуле Шифринсона

Нетрудно видеть, что формулы Стокса, Блазиуса и Шифринсона могут быть представлены зависимостью одного вида

где А, т — коэффициенты, величина которых для каждой зоны трения неизменна.
Однако формула Альтшуля к этому виду не приводится. Это исключает возможность решения гидравлических задач в общем виде.
Ту же задачу можно было решить следующим образом. При Re = ReI еще справедлива формула Блазиуса, а при Re = RеI уже можно пользоваться формулой Шифринсона. Учитывая, что переходные числа Рейнольдса Альтшулем рекомендовано находить по формулам:
для зоны смешанного трения получаем:

Поделив почленно получим:


Различие в выражениях для расчета коэффициента А объясняется тем, что в первом случае не было сделано необходимое алгебраическое преобразование

Среднеквадратичная погрешность аппроксимации В.ДБелоусова по сравнению с формулой Альтшуля составляет около 5%. Связано это, в частности, с тем, что ее автор не стремился сделать погрешность вычислений минимальной, а исходил из условия равенства коэффициентов X на границах зоны смешанного трения и соседних зон.
Автору совместно с аспиранткой Н.В. Морозовой удалось свести уравнение Альтшуля к виду со среднеквадратичной погрешностью 2,6%. Это было сделано следующим образом.
Представим формулу Альтшуля в виде

- Недостатком данной записи является то, что расчетный коэффициент 0,11(68 + ε · Re) °-25 является функцией числа Рейнольдса. Вместе с тем из формул следует, что в зоне смешанного трения справедливо неравенство
- 10 Читайте также: Круглошлифовальные станки по металлу
В ней значения R приведены с достаточно подробным шагом по G, в среднем 5–10 т/ч, а на малых расходах даже ниже. Тем не менее, может потребоваться вычисление удельных потерь для промежуточных скоростей и расходов. Для этого необходима интерполяция таблицы.
Но если расчет проводится с применением ЭВМ, например, с использованием электронных таблиц MS Excel, что очень удобно, так как гидравлический расчет трубопроводов всегда записывается в табличной форме, целесообразно иметь простую и в то же время достаточно точную формулу для R.
По физическим соображениям, однако, такая формула должна составляться относительно внутреннего диаметра dв, который можно определить по величине dн и δ с использованием данных ГОСТ 10704. В руководстве [1] и других источниках приводятся известные из гидравлики общие выражения для R через коэффициент гидравлического трения, но они достаточно сложны для массовых инженерных расчетов.

Если построить по данным табл. 9.11 из [1] номограмму для R (рис. 1), можно увидеть, что при изображении в логарифмических координатах она представляет собой набор прямых линий.
Это означает, что величина R должна находиться в степенной зависимости от параметров w (или G) и dв. Подобная номограмма содержится и в работе [1].
В результате обработки с помощью метода наименьших квадратов таблица хорошо аппроксимируется формулой:

дающей для наиболее употребительного в практике проектирования диапазона скоростей 0,8–2,5 м/с и наружных диаметров в пределах 108–325 мм погрешность не более 0,15 %.
При крайних значениях данных параметров отклонение не превысит 0,5 %, что также заведомо находится в области обычной погрешности инженерных расчетов. Соотношение (1) справедливо при величине среднего значения плотности воды 940 кг/м3, характерной для температур в теплосетях [1].
При других плотностях необходим пропорциональный пересчет. С учетом связи между скоростью и расходом воды и сечением трубопровода получаем:

Здесь уже результат непосредственно от плотности зависеть не будет, поскольку она входит в уравнение неразрывности потока, которое было использовано при переходе от (1) к (2), и в процессе преобразований сокращается.
Нетрудно заметить, что выражение (2) весьма напоминает как по форме, так и по числовым коэффициентам, в том числе уровню показателей степени при w и dв, полученную ранее автором зависимость [2, 3] для потерь давления в стальных водогазопроводных трубах, используемых в системах водяного отопления (3):
![]()
В то же время отсюда можно сделать вывод об определенном различии режима течения воды в системах отопления и теплоснабжения — в первом случае он является переходным между режимом гидравлической гладкости и зоной квадратичного сопротивления, а во втором имеет место чисто квадратичная зона.
Это связано с более высокой эквивалентной шероховатостью труб теплосетей kэ, равной 0,5 мм, то есть 5 × 10–4 м [1], по сравнению с трубопроводами систем отопления (0,2 мм [4]) и с увеличенными скоростями воды, характерными для теплосетей, а также с ее меньшей вязкостью из-за повышенной температуры. В самом деле, для наименьших использованных значений dв = 125 мм = 0,125 м и скорости w = 0,8 м/с величина критерия Рейнольдса Re будет равна
![]()
Здесь 0,0002376 Па⋅с — динамическая вязкость воды при плотности 940 кг/м3 [5]. Если теперь вычислить соотношение Re kэ/dв, получим
![]()
что значительно больше предельного значения, характеризующего окончательный переход к квадратичному режиму сопротивления [5]. При более высоких скоростях уровень Re kэ/dв будет еще выше, а значит, и режим течения заведомо остается в квадратичной зоне. Диаметр трубопроводов на полученные выводы при этом не влияет, поскольку сокращается при расчете комплекса Re kэ/dв.
Для сравнения отметим, что для внутреннего водопровода средний показатель степени при w равен 1,76 [6], что практически соответствует гидравлически гладким трубам, поскольку в этом случае известная формула Блазиуса дает значение этого показателя, равное 1,75.
Если теперь провести технико-экономическую оценку аналогично выполненной в [7] для систем отопления, окажется, что в силу квадратичного режима сопротивления оптимальная скорость воды в трубопроводах теплосетей wопт уже не будет зависеть от G, а величина оптимального диаметра dв.
опт будет строго пропорциональна √G.
Формула для dв.опт при wопт около 0,9 м/с в этом случае получается в следующем виде, где G следует подставлять в [кг/ч]:
dв.опт = 0,6√G, мм. (4)
Это меньше, чем для отопления, а wопт, напротив, значительно выше (примерно в 1,5 раза), главным образом, из-за гораздо более высокого КПД сетевых консольных насосов по сравнению с циркуляционными, как правило, выполненными с «мокрым ротором». Вследствие этого для теплосетей становится выгоднее уменьшать капитальные затраты на трубопроводы, поскольку расход электроэнергии на привод насосов при этом будет расти медленнее, чем в отопительных системах.
Таким образом, формулы, приведенные в настоящей работе, очень просты, наглядны и доступны для инженерных расчетов, особенно при использовании электронных таблиц MS Excel, а также в учебном процессе.
Их применение позволяет отказаться от интерполяции таблиц при сохранении точности, требуемой для инженерных расчетов, и непосредственно вычислять удельное сопротивление трубопроводов в широком диапазоне скоростей и расходов воды и диаметрах вплоть до dн = 325 мм.
Этого вполне достаточно для проектирования водяных тепловых сетей в большинстве современных случаев.
МНЕНИЕ
Валентин Воропаев, главный специалист по теплоснабжению ООО «Миран-Проект»: «В практике проектирования инженерных систем зданий мы, проектировщики, сталкиваемся с гидравлическими расчетами различных систем, будь то система отопления, система горячего водоснабжения, холодоснабжения и так далее, а также с гидравлическими расчетами наружных сетей — как теплоснабжения, так и водопровода. И для этих расчетов приходится пользоваться различными таблицами в разных справочниках. Поэтому я могу только приветствовать появление методики, позволяющей автоматизировать разные гидравлические расчеты. А если еще в этой методике будут учтены различные режимы, среды и материалы трубопроводов, то получится очень неплохой и удобный справочник, облегчающий жизнь проектировщикам».
Потери напора в трубопроводе по длине и местные: расчет по формулам и таблицам Шевелева
Третья статья в цикле статей по теоретическим основам гидравлики посвящена определению потерь напора.
Как рассказывалось ранее, при своем движении жидкость испытывает сопротивление, что выражается затратами ее энергии, т.е. затратами ее напора, что называют потерями напора.

Два вида потерь напора
Потери напора принципиально делятся на два типа:

Потери напора: местные (обведены кружком) и по длине
- Местные (на рисунке обведены красным)
- Потери по длине (на рисунке подчеркнуты зеленым)
Местные потери конкретно на данном рисунке: поворот, задвижка (условное обозначение по ГОСТ – «бантик»), еще один поворот и внезапное (т.е. не плавное) расширение.
Потери по длине здесь – это потери на прямолинейных участках l1, l2, l3, l4.
Местные потери
Местные потери напора (говорят также «потери напора на местные сопротивления«) – это потери напора, которые происходят в основном из-за вихреобразования в конкретных местах трубопровода (потому и «местные»).
Любое препятствие на пути движения потока жидкости является местным сопротивление. Чем сильнее деформируется поток, тем больше будет потеря напора. Например, на рисунке ниже показано внезапное сужение трубопровода.
Хорошо видны 4 вихревые зоны до и после сужения.

Местное сопротивление — внезапное сужение
Местную потерю напора можно определить, зная коэффициент сопротивления для данного сопротивления (обозначается буквой дзэта ζ, не имеет размерности) и среднюю скорость потока в сопротивлении V.
(g – ускорение свободного падения, g = 9,81 м/с2 , для быстрых подсчетов можно округлить до 10 м/с2)
Пример. Определить потерю напора в вентиле, установленном на трубе внутренним диаметром d = 51 мм, при расходе Q = 2 л/с.
Сначала по уравнению неразрывности (ссылка на статью 2) определим среднюю скорость движения жидкости.
V = Q / ω = 4 · Q / 3,14 · d² = 4 · 0,002 / 3,14 · 0,051² = 0,98 м/с
Теперь необходим коэффициент сопротивления вентиля. Такие данные берут из гидравлических справочников или у производителей конкретной арматуры. По справочным данным находим, что коэффициент местного сопротивления вентиля равен 6.
Тогда потеря напора на вентиле: hвент = ζ · V²/ 2 · g = 6 · 0,98² / 2 · 10 = 0,29 м.

Иллюстрация местных потерь напора
При расчете трубопроводных систем (внутренний водопровод здания, наружная водопроводная сеть и т.п.
) обычно высчитывают не все сопротивления (так как их может быть очень много), а только самые существенные, создающие наибольшие сопротивления: например, счетчик воды.
Потеря напора на остальных местных сопротивлениях учитывается коэффициентом, на который умножается значение потерь напора по длине (1,05 – 1,15 для наружных сетей, 1,1 – 1,3 для внутренних сетей здания).
Потери по длине
Потери напора по длине – потери напора на участках трубопровода. Возникают из-за работы сил трения. (сила трения возникает между слоями движущейся жидкости). Величина потерь напора, также, как и местных потерь, напрямую зависит от скорости движения жидкости. При достаточно высокой скорости усиливается влияние шероховатости стенок трубы.

Потерю напора по длине можно увидеть по разнице в уровнях воды между двумя пьезометрами
Точное определение потерь напора по длине является довольно сложной задачей, для этого необходимо устанавливать режим движения жидкости (бывает ламинарный и турбулентный), подбирать расчетную формулу для коэффициента гидравлического трения в зависимости от числа Рейнольдса Re, характеризующего степень турбулизации потока. Это изучается студентами в рамках курса механики жидкости.
При этом для быстрого расчета потерь напора были составлены специальные таблицы для инженеров, позволяющие, зная материал трубы и ее диаметр, а также расход воды, быстро определить так называемые удельные потери напора (сколько напора теряется на 1 м трубы).
Эта величина называется 1000i, значение 1000i = 254 означает, что поток, проходя 1 м такой трубы теряет 254 мм (миллиметра) напора, т.е. 0,254 метра. Это значение также называется «гидравлический уклон», и это нельзя путать с геодезическим, т.е. просто с физическим уклоном (наклоном) самой трубы.
Для расчета стальных труб используют таблицы Шевелева.
Скачать таблицы таблицы Шевелева в формате PDF можно на нашем сайте.
Таблицы Шевелева для определения потерь напора

Например, из данного фрагмента видно, что если вода с расходом 1,50 л/с пойдет по трубе диаметром 50 мм, то скорость в этой трубе будет 0,47 м/с, а 1000i составит 9,69 мм на метр (на каждом метре трубы теряется 9,69 миллиметров напора).
Давление в точке жидкости — решение задачи по гидравлике
Чтобы определить, сколько метров напора будет потеряно на всем участке – нужно перемножить 1000i с длиной участка. Чтобы ответ получился в метрах, 1000i делят на 1000.
- Итак, потери напора по длине: hl = 1000i·l / 1000 = i·l
- Если наш участок трубы имеет длину, скажем, 25 метров, то потеря напора на нем:
- hl = 9,69*25/1000 = 0,24 м.
- Учтем и местные сопротивления, тогда полная потеря напора на данном участке:
- hl = 0,24*1,3 = 0,31 м.
Таблицы были переведены в электронный вид в виде программы, созданной Любчуком Ю.Е. Загрузить программу «Таблицы Шевелева» можно с нашего сайта.
С помощью этой программы, можно легко посчитать потери напора в трубах из различных материалов. В следующей статье подробно опишем, как пользоваться данной программой на задаче из жизни.
Гидравлический расчет трубопровода – Проф Трубы

26.02.2019
- 1 Введение
- 2 Расчетная часть
- 3 Заключение
Трубопровод как способ транспортировки жидких и газообразных сред является самым экономичным способом во всех отраслях народного хозяйства. А значит он всегда будет пользоваться повышенным вниманием у специалистов.
Гидравлический расчет при проектировании трубопроводной системы позволяет определить внутренний диаметр труб и падение напора в случае максимальной пропускной способности трубы. При этом обязательным является наличие следующих параметров: материал, из которого изготовлены трубы, вид трубы, производительность, физико-химические свойства перекачиваемых сред.
Производя вычисления по формулам, часть заданных величин можно взять из справочной литературы. Ф.А.Шевелев, профессор, доктор технических наук разработал таблицы для точного расчета пропускной способности.
Таблицы содержат значения внутреннего диаметра, удельного сопротивления и др параметры. Помимо этого, существует таблица приближенных значений скоростей для жидкостей, газа, водяного пара для упрощения работы с определением пропускной способности труб.
Используется в коммунальной сфере, где точные данные не столь необходимы.
Способ установки гидравлических трубопроводов
Расчетная часть
- Расчет диаметра начинается с использования формулы равномерного движения жидкости (уравнение неразрывности):
- q = v*ω,
- где q — расчетный расход
- v — экономическая скорость течения.
- ω — площадь поперечного сечения круглой трубы с диаметром d.
- Рассчитывается по формуле:
- ω = πd² / 4,
- где d — внутренний диаметр
- отсюда d = √4*q/ v*π
Скорость движения жидкости в трубопроводе принимается равной 1,5-2,5 м/с.
Это то значение, которое соответствует оптимальной работе линейной системы.
- Потери напора (давления) в напорном трубопроводе находят по формуле Дарси:
- h = λ*( L/ d)*( v2/2g),
- Как проводится гидравлический расчет
- где g — ускорение свободного падения,
- L — длина участка трубы,
- v2/2g — параметр, обозначающий скоростной (динамический) напор,
λ — коэффициент гидравлического сопротивления, зависит от режима движения жидкости и степени шероховатости стенок трубы. Шероховатость подразумевает неровность, дефект внутренней поверхности трубопровода и подразделяется на абсолютную и относительную. Абсолютная шероховатость — это высота неровностей. Относительную шероховатость можно рассчитать по формуле:
Шероховатость различна по форме и неравномерна по длине трубы. В связи с этим в расчетах принимается усредненная шероховатость k1 — поправочный коэффициент.
Данная величина зависит от целого ряда моментов: материал труб, длительность эксплуатации системы, различные дефекты в виде коррозии и др. При стальном исполнении трубопровода значение применяется равным 0,1-0,2 мм.
В то же время, в иных ситуациях параметр k1 можно взять из таблиц Ф.А.Шевелькова.
- В том случае, если длина магистрали невысока, то местные потери напора (давления) в оборудовании насосных станций примерно одинаковы потерям напора по длине труб. Общие потери определяются по формуле:
- h = P/ρ*g, где
- ρ — плотность среды
Случаются ситуации, когда трубопровод пересекает какое-либо препятствие, например, водные объекты, дороги и др. Тогда используются дюкеры — сооружения, представляющие собой короткие трубы, прокладываемые под преградой. Здесь тоже наблюдается напор жидкости. Диаметр дюкеров находится по формуле (с учетом, что скорость течения жидкости составляет более 1 м/сек):
- h = λ*( L/ d)*( v2/2g),
- h = I*L+ Σζ* v2/2g
- ζ — коэффициент местного сопротивления
Разность отметок лотков труб в начале и конце дюкера принимается равной потерям напора.
- Материал для гидравлических трубопроводов
- Местные сопротивления рассчитываются по формуле:
- hм = ζ* v2/2g.
Движения жидкости бывают ламинарные и турбулентные. Коэффициент hм зависит от турбулентности потока (число Рейнольдса Re). С увеличением турбулентности создаются дополнительные завихрения жидкости, за счет чего величина коэффициента гидравлического сопротивления увеличивается. При Re › 3000 всегда наблюдается турбулентный режим.
Коэффициент гидравлического сопротивления при ламинарном режиме, когда Re ‹ 2300, рассчитывается по формуле:
В случае квадратичности турбулентного потока ζ будет зависеть от архитектуры линейного объекта: угла изгиба колена, степенью открытия задвижки, наличием обратного клапана. Для выхода из трубы ζ равна 1. Длинные трубопроводы имеют местные сопротивления порядка 10-15% на трение hтр. Тогда полные потери:
Производя расчеты, выбирается насос, исходя из параметров подачи, напора, действительной производительности.
Заключение
Гидравлический расчет трубопровода вполне возможно произвести в онлайн-ресурсе, где калькулятор выдаст искомую величину. Для этого достаточно ввести в качестве исходных величин состав труб, их длину и машина выдаст искомые данные (внутренний диаметр, потери напора, расход).
Помимо этого, существует онлайн версия программа «Таблицы Шевелева» ver 2.0. Она проста и удобна в освоении, является имитатором книжного варианта таблиц и также содержит калькулятор подсчета.
Компании, занимающиеся прокладкой линейных систем, имеют в своем арсенале специальные программы для расчетов пропускной способности труб. Одна из таких «Гидросистема» разработана российскими программистами, популярна в российской же промышленности.
Самостоятельный гидравлический расчет трубопровода
Гидравлический расчет паропровода
Калькулятор позволяет провести гидравлический расчет участка паропровода и определить потери давления в паропроводе насыщенного пара по методике «Сборник задач по теплофикации и тепловым сетям», А.П. Сафонов, Москва, ЭнергоАтомИздат, 1985.
Общие данные
Гидравлический расчет участка паропровода проводится в два этапа:
-
- предварительный этап (предварительный расчет давление пара в конце участка при известном давлении пара в начале участка);
- уточняющий этап (определение свойств пара в середине участка с учетом давления в конце участка и пересчет потерь давления на участке).
- Протяженность участка паропровода, массовый расход пара, сортамент трубы, сумма местных сопротивлений на участке, эквивалентная абсолютная шероховатость внутренней поверхности стенки трубы и удельные тепловые потери задаются в исходных данных.
- Сумму коэффициентов местных сопротивлений на участке можно определить по справочным данным.
- Эквивалентную абсолютную шероховатость внутренней поверхности стенки трубы можно определить по справочным данным.
- Удельные тепловые потери на 1 метр паропровода можно:
-
- определить расчетом согласно СП 61.13330.2012 «Тепловая изоляция оборудования и трубопроводов» исходя из принятой конструкции теплоизоляции;
- принят равными нормам плотности теплового потока оборудования и трубопроводов согласно п.6.1.2 СП 61.13330.2012 «Тепловая изоляция оборудования и трубопроводов».
- Коэффициент гидравлического трения рассчитывается автоматически.
- Плотность и кинематическая вязкость насыщенного пара определяется по справочным данным автоматически.
- При проведении расчета необходимо контролировать скорость пара в паропроводе.
Количество строк: 5,10,20 Скачать таблицу: Поделится ссылкой на таблицу:
Результатом гидравлического расчета паропровода является определение при заданных исходных данных и выбранном диаметре паропровода:
-
- потерь давления на участке паропровода;
- количества конденсата, образующегося на участке паропровода;
- давления пара в конце участка паропровода;
- скорости пара в начале участка паропровода;
- средней скорости пара в паропроводе.
Примечание
Гидравлический расчет паропровода выполнен в виде длиной цепочки каскадных расчетов (друг за другом), поэтому расчет занимает некоторое время с перерасчетом промежуточных значений. Рекомендуется выждать время для получения окончательного значения.
В комментарии приветствуются пожелания, замечания и рекомендации по улучшению программы.
Источник https://sozidau.ru/tablitsa-gidravlicheskih-poter-dlya-trub/
Источник https://tokarmaster.ru/sovety/formuly-dlya-raschetov-poteri-davleniya-v-truboprovode.html
Источник



